The Scientific Gamer

I’m back! (Back! Back.) And for the first of many new scienceposts, I bring you a quick précis of what I just spent the last week doing. I feel somewhat tawdry doing this since it’s duplicating my space school research more than a little bit, but what the hell – it’s my research*, and since I had to aim the task at eleven year olds I didn’t get to use all of it.

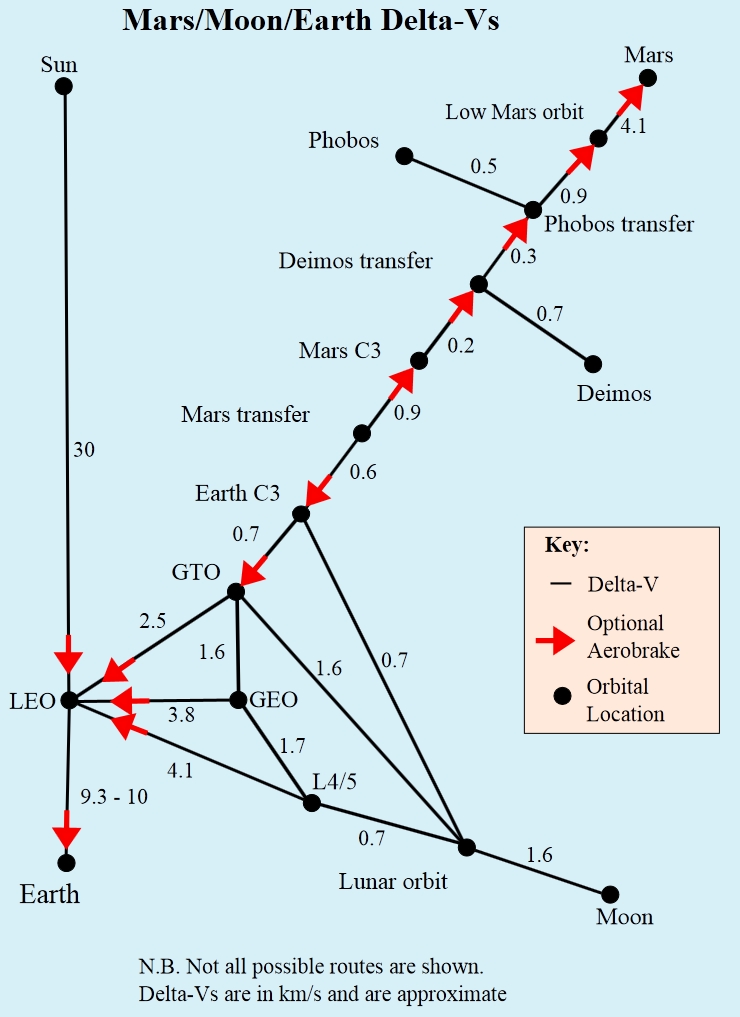
We’ll start with this really great chart featured on wikipedia’s page on space colonisation.

Delta-v is the fancy space scientist way of saying “change in velocity”. Objects that are stationary with respect to the thing you are trying to reach or get away from have zero delta-v. A spacecraft sitting on the launchpad on Earth has zero delta-v with respect to Earth orbit. To get it up to LEO, we are going to have to change its delta-v by around 10 km s^-1 to accelerate it to the orbital velocity of 8 km s^-1 required to stay in low Earth orbit. Where do the additional 2 km s^-1 of delta-v come from, if we only need to get it up to 8 km s^-1? That’s extra delta-v needed to counteract the effects of atmospheric drag and gravitational forces during the spacecraft’s ascent. Delta-v is basically a measure of the amount of “effort” needed to move from one orbit to another – or one place to another – on the part of the spacecraft engine, which typically burns propellant to create reaction mass to produce delta-v.

The thing about delta-v is that it’s not an absolute measure. It takes no notice of spacecraft attributes like payload weight or fuel weight which make the amount of thrust required from the spacecraft engine different from spacecraft to spacecraft. It tells you nothing about the specific amount of effort you’re going to have to make to get a specific spacecraft into space; in order to get that we’d have to take these specific spacecraft attributes and multiply them by the delta-v required in order to get a specific required thrust value unique to that spacecraft. Once we’ve done that we can’t then take that thrust value and apply it to another spacecraft because its weight, engine, structure etc. will be all different. We’d have to recalculate the thrust value using that spacecraft’s own attributes.

What delta-v does do, though, is provide a quick and easy scalar quantity that allows spacecraft designers to estimate how difficult a particular orbital maneuver will be relative to what it’s already done, or has yet to do. The above chart is a summary of the delta-v budget required to get to various places in the solar system from other places in the solar system. By looking at it we can see that getting from Earth to LEO is rather hard, requiring a delta-v of 9.3 km s^-1 (yeah I rounded up before, so sue me), but that getting from the LEO altitude of just 300 km up all the way out to the Moon requires a total delta-v of just 4.8 km s^-1. In other words, no matter what spacecraft you’re dealing with and how heavy it is, it’s always going to take twice as much effort to cover the first 300 kilometres from the surface of the Earth to LEO as it is to travel the next 380,000 km out to lunar orbit.

The reason I like this chart so much is because it illustrates a key restriction on travelling around the solar system that I’ve brought up more than a few times before on here: by far the hardest part of space travel is getting out of the Earth’s gravity well. Once you’ve done that you can get about on relatively little fuel because the subsequent delta-v requirements are comparatively low, but while the Earth provides a rather pleasant living environment for human beings – it doesn’t burn us, freeze us, crush us, poison us or suffocate us, unlike literally everywhere else in the universe – being stuck at the bottom of its gravity well is actually a crippling handicap as far as space travel is concerned. When the amount of energy you have to expend travelling those first 300 km is only slightly less than the amount of energy you’d expend getting from there to freakin’ Mars, you know you have a problem.

 As long as spacecraft manufacturing and launch facilities remain Earthbound – as they are likely to do for the foreseeable future – human exploration of the solar system and beyond is always going to be held back by this massive delta-v requirement to get out of the gravity well. Earth’s gravity is not something that can be counteracted, cancelled out or removed; as long as we launch stuff from its surface we’re always going to have to use these massive, inefficient rockets to provide that large initial delta-v investment. The only thing we can do about it is move somewhere else, building and launching our spaceships from locations which are a little kinder in terms of delta-v requirements such as geostationary orbit or even the surface of the Moon. As you can imagine, creating the sort of offworld industrial base required to do this is going to be a bit of a stretch considering we can hardly claim to have conquered even LEO with the ISS.

Some additional notes about the chart: “C3” is another way of saying escape velocity, so the Earth C3 and Mars C3 points on the chart are the Earth and Martian escape velocities respectively. The reason the Mars C3 point comes right after the Earth C3 one is because you can follow the chart back in the other direction, using it to go from Mars to low Mars orbit to Mars escape velocity, and that allows you to get a rough value for the amount of delta-v required to get back to Earth.

 Another crucial point about delta-v is that you need it to slow down as well as speed up a spacecraft. Accelerating up to the Martian escape velocity is no good whatsoever if you don’t have the fuel left to slow the spacecraft down again once it arrives back at Earth. Fortunately, if you happen to be going to – or even passing by – a large planetary body with a sufficiently thick atmosphere, you can slow the spacecraft down effectively “for free” expending just a bare minimum of fuel by using a maneuver called aerobraking. Here we make atmospheric drag forces work for us for once; by adjusting the spacecraft trajectory so that it skips through part of the planet’s atmosphere, the drag forces that arise from this will slow the spacecraft down for us with no further effort required on our part to change its velocity. The amount of time it spends within the atmosphere depends on how much we want to slow it down; if we want to stop it entirely then we just do a stock re-entry procedure. This free delta-v is one way only – you can use it to get from LEO back to Earth, but you can’t use it to get from Earth to LEO – and that’s denoted on the chart by the giant red arrows.

Finally, now that we understand how delta-v works it should be obvious why we use the quantities of impulse and specific impulse to describe rocket engines and their thrust efficiency rather than force or energy or any of that jazz. Thrust exerts a force on the spacecraft according to F = mass times acceleration. To achieve a certain change in velocity we’re going to have to accelerate it over a sustained period of time — so to get to 1 km s-1 we accelerate it at 1 m s-2 for 1000 seconds or something — and since impulse equals force multiplied by the time you apply that force for, once you factor out the spacecraft mass (so divide the thrust force F by m) you end up with acceleration multiplied by time, and that is just another way of saying delta-v.

*By which I mean “It’s my shameless cribbing from Wikipedia.”