Blah blah blah transit of Venus blah blah blah once in a lifetime event blah blah astonishing photographs blah. Screw that astronomy shit, let’s do some real science.
Why is the transit of Venus important? It’s less so than it was, but in the 18th century it was very important because it provided astronomers with the first practical method of measuring the distance separating the Earth from the Sun. This is a much bigger deal than it sounds; until this measurement was taken we were in the situation of not knowing for sure how far away anything in the Solar System was, because while we knew a lot of relative distances – i.e. we know planet X is twice as far away from the Sun as we are, and we know planet Y is three times as far away from the Sun as we are – we had nothing absolute. There was nothing we could point to and say “Yes, we know for sure that this distance is X number of metres,” or whatever. Getting the distance between the Earth and the Sun would allow us to easily figure out the distance between the Sun and all the other planets, not to mention eventually allowing us to determine the distance separating us from the nearest stars, but measuring out the length of that first cosmic yardstick with which to scale everything else is an incredibly big deal because it’s so goddamn hard.
The problems are similar to the ones I mentioned in my post on stellar measurement; without doing something very clever there’s no real way of determining how big something is in space. It could be a big thing far away or a small thing close up, and telling the difference is nigh-impossible making it very very difficult to measure even interplanetary distances without modern technology like radar. Not knowing the numbers behind the basic structure of the Solar System kind of puts a crimp on our properly understanding it, so getting this one measurement of the Earth-Sun distance – and by inference, all other planet-Sun distances – was very important. Happily there was a way of doing it in the eighteenth century without having to wait two hundred years for radar, and the methodology was similar to the parallax method used to measure the distance to the nearest stars.
The idea is that at its closest point of approach (i.e. between the Earth and the Sun) Venus will be close enough that, if observed from different points on the Earth’s surface, it will appear to be located in different positions in the sky due to the difference in viewing angle between the observers. Most of the time this isn’t that useful because you need a fixed background against which to track Venus’ movement; however, during a transit Venus is silhouetted against the Sun, which acts as a reference point and allows us to do this:
Send out lots of different observers to locations all over the world and get them to note down what they see when Venus transits the Sun. Gather together all their information. Compare the differences in the observed position of Venus with the differences in position of the observer. Work out the parallax angle α from the shift in the apparent position of Venus. Use the parallax angle α and known distance d separating the observers to work out the distance between the Earth and Venus.
This sort of thing took an incredible amount of effort to pull off in the eighteenth century (especially since the Seven Years’ War was going on at the time) and the story of the attempt to measure the 1761 and 1769 transits is littered with tragic-comical failures like this guy. However, after nearly a decade of work astronomers did eventually get some good measurements of the transit and calculated the distance separating the Earth and Venus. Unfortunately, this on its own isn’t that useful. Because the Earth and Venus aren’t gravitationally bound at all we can’t use that information to infer anything else about the rest of the Solar System. What we need to do is somehow use the Earth-Venus separation to figure out either the Earth-Sun distance or the Venus-Sun distance, since those actually are useful.
Enter Kepler’s third law. Kepler’s laws are a set of relationships governing the behaviour of orbiting bodies, and the third law states that
The square of the orbital period of any planet is proportional to the cube of the semimajor axis of its orbit.
What the hell does this mean? The orbital period of a planet is the amount of time it takes to go around the Sun once – i.e. one year for that planet. The semimajor axis is… basically it’s the distance separating the planet and the Sun, although it’s a little more complicated than that. Expressed mathematically Kepler’s third law is
where P is the period, a is the semimajor axis and the funny thing separating them is a mathematical operator meaning “proportional to”. In other words, P2 is equal to a3 multiplied by some constant of proportionality k – if k is 2, then P2 is always twice a3, and so on.
(This graph expresses Kepler’s third law visually and may help to give some idea of what the hell I’m jabbering on about here.)
Now, while the orbital periods of all the planets were known in the 18th century (we could see the damn things, after all) astronomers had no idea what the constant of proportionality k was. It could have been anything, and without knowing what that constant was we were unable to determine the semi-major axes from the period alone. However, we did know that the constant of proportionality — whatever it actually turned out to be — was the same for all planets. Or in other words
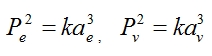 Where Pe is the orbital period of the Earth, Pv is the orbital period of Venus etc. etc. No matter what planet you’re dealing with k doesn’t change, and this lets us do some really convoluted rearranging to get
Where Pe is the orbital period of the Earth, Pv is the orbital period of Venus etc. etc. No matter what planet you’re dealing with k doesn’t change, and this lets us do some really convoluted rearranging to get
Where T is the distance between the Earth and Venus as measured from the transit. This looks awful, but since T, Pe and Pv are all known quantities it all boils down to
We can figure out the semi-major axis of the Earth based on the distance between the Earth and Venus. Furthermore, we can use this number to work out the constant of proportionality k mentioned in Kepler’s third law above, and from that and their orbital periods we can work out the distance separating the Sun and every other planet in the solar system, not to mention eventually being able to use the astronomical unit derived from this to determine the distance to the nearest stars. Not bad for a decade’s work.




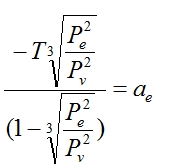
Hehe very nice. Been some time since my physics lessons