Hey, so you know when I said that in order for the universe to accommodate the speed of light being invariant something else has to pick up the slack, and that something is time?
I lied.
Or at least I was economical with the truth because that post on time dilation was getting on for 3000 words. The invariance of light speed in fact has knock-on effects for most of the dimensions of space-time as well as things like mass and energy, and in this post I’m going to focus on what relativistic speeds do to an object’s size – otherwise known as Lorentz contraction.
We’re mostly going to stay away from the horrible maths this time because I get the feeling most people aren’t able – or willing – to follow that all the way through, so I’ll do the whole ripping-off-a-plaster thing and get what we have to do out of the way quickly. After looking at the light clock we derived the following expression for time dilation
The 1/√(1-v2/c2) term is actually something called the Lorentz factor γ, which crops up a hell of a lot in equations dealing with special relativity. For example, when dealing with the length of an object in a stationary moving frame x versus a moving (dilated/relativistic) reference frame xd, we say that
which honestly makes the whole thing much easier to deal with if it’s a simple matter of multiplying the stationary, or “rest” mass/length/time by this common Lorentz factor to get the dilated/contracted version.
Anyway, what this implies is that just as time slows down compared to a stationary observer as an object reaches relativistic speeds, the object will also contract in size along the axis of travel (i.e. a train would contract down the long axis of its length rather than in width or height). This phenomena is known as length contraction, or Lorentz contraction, and I’m bringing it up because it poses an interesting paradox that has consequences for our concept of simultaneity (i.e. the concept that it can be 5 o’ clock everywhere at the same time).
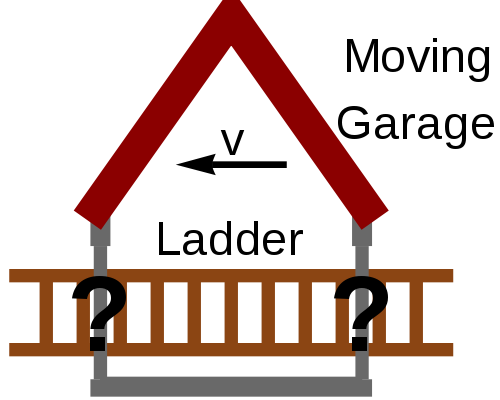
Wikipedia explains this paradox as the Ladder paradox; it was taught to me with a medieval knight riding a charger carrying a lance in place of the ladder, but honestly any long horizontal object will do for this thought experiment. The idea is, you have a man carrying a ladder running very very quickly towards a garage. The garage has a door at either end, and the length of the garage is just slightly shorter than the length of the ladder when it is at rest. The front door of the garage is open and the rear door of the garage is shut. The man runs into the garage. When the ladder is fully inside the garage, the front door immediately slams shut and the rear door opens, allowing the man to exit the garage without running into the door and becoming a nasty relativistic smear across its surface.
Now, this thought experiment is already a bit of a brain twister; the length of the garage is smaller than the rest length of the ladder, so if the front and rear doors open/close simultaneously and they are not both open at once there is no possible way the ladder can fit inside the garage – unless the ladder is moving at a relativistic velocity sufficient to contract its length so that it can. Everyone with me so far?
The problem here – and the paradox – lies in the frames of reference I was jabbering about last week. From the point of view of the garage, the ladder shrinks in length and can easily fit inside it with no problems. However, just because we happen to think of the garage as the stationary object doesn’t mean that this is the one true reference frame. The ladder is also valid frame of reference, and from the point of view of the ladder it’s the garage which is moving towards it at a relativistic velocity, and hence the garage which shrinks and contracts in length.
The paradox is this, then: from the point of view of the garage, the ladder shrinks in length and everything is okay, but from the point of view of the ladder the already-too-small garage contracts in length even further while the ladder remains far too long to fit inside it. How on earth is the ladder supposed to make it through the garage in this reference frame?
There is an answer to this (or else special relativity would have come crashing down by now) and that answer is to throw out the concept of absolute simultaneity. In the garage’s reference frame the front door closes and the back door opens at exactly the same time – simultaneously. However, this is not the case for the ladder’s reference frame. The ladder sees things differently. From the ladder’s point of view, the back door opens first, allowing the front end of the ladder to pass through without any problems. Then, when the back end of the ladder has passed the front door, the front door slams shut. The back door opening and the front door closing happen at different times; the simultaneous events in one frame of reference happen at different times in another. This demonstrates the relativity of simultaneity, or as Wikipedia puts it:
According to the special theory of relativity, it is impossible to say in an absolute sense whether two distinct events occur at the same time if those events are separated in space, such as a car crash in London and another in New York. The question of whether the events are simultaneous is relative: in some reference frames the two accidents may happen at the same time, in other frames (in a different state of motion relative to the events) the crash in London may occur first, and in still other frames the New York crash may occur first.
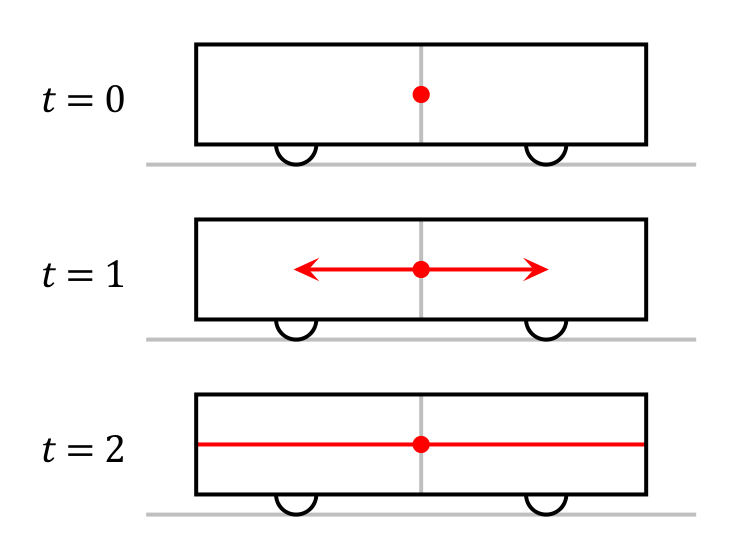
In order to demonstrate the whys behind this we’re going to use a thought experiment similar to last week’s light clock, only this time our moving object is a train whizzing past a stationary platform.
There is a lamp in the centre of the train carriage. The lamp is turned on and light emerges which illuminates the train carriage. This seems fairly uncontroversial, but the way this happens will be perceived slightly differently by an observer standing next to the lamp and an observer standing on the station platform.
The observer standing next to the lamp is moving at the same velocity as the lamp and is stationary with respect to it. He sees the light moving as we would expect; the light covers the equal distances to either end of the train carriage at the same speed, and the light reaches the ends of the train carriage simultaneously.
However, to the observer standing on the station platform the lamp is moving. Once the lamp is switched on the rear of the traincar will be moving towards the emitted light, while the front of the traincar will be moving away from it. Since the speed of light c is invariant in all reference frames (as we saw last week) the light will travel towards the rear of the carriage at the same speed as it does for the moving observer, except because the rear of the carriage is moving towards the light the light will have a shorter distance to travel. Thus to the observer on the station platform the light will appear to hit the rear of the train carriage first, and the front of the train carriage second. QED.
This, I hope, dovetails nicely with the time dilation post to show that time isn’t the immutable constant we’re all used to in everyday life. Depending on where you are and how fast you’re going it can be bent and stretched and tied in knots. You pays your money and you takes your frame of reference.


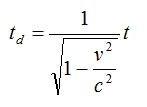
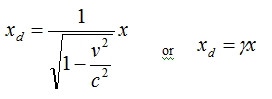



I like the thought experiments and I get what is going on. I do thoroughly understand it conceptually and theoretically…
But is there a good example that may be readily available to a casual individual to observe? As in, can the train thing be done in real life and is it something that would be obvious (or obvious when pointed out or whatever) to us?
No. Thought experiments are thought experiments for two reasons: 1) To make the concepts they describe easy to understand, 2) Because no practical method of carrying out the thought experiment in the real world exists. We can indirectly observe the results of supernova, the behaviour of light, subatomic particle reactions etc. and see the hand of special relativity there, but it’s mostly not something you can look at in the way described above.
http://en.wikipedia.org/wiki/Tests_of_special_relativity has a good summary of technical verifications of special relativity in the laboratory, but we don’t run ladders through garages at light speed. Sorry.
I demand you make it so this happens. Demand it. Science must answer to me!
Until I see you running a ladder through a garage at light speed I refuse to believe any of this is true.
Thats wy you will remain a smurf and never become a giant