RRRrrrrrssssssssssnnnnnncccccccceeee.
I’m sorry, I was doing an impression of a resonating object there, mainly because I feel that starting with a description of what resonance is would be pointless. Everyone knows what “to resonate” means, and as far as physical principles goes all schoolchildren get taught about Galileo Galilei and oscillating pendulums when they’re doing their GCSEs. Basically if you have something undergoing a persistent, periodic motion, then it will transfer and store energy with more efficiency at certain specific frequencies resulting in a greater amplitude of motion. Most people understand this in the context of pendulums, as above – where, if you release a pendulum and let it settle for a few seconds, it will eventually swing with a period 
where l is the length of the pendulum and g is the pendulum’s acceleration due to gravity.
In a constant gravitational field – say, at the surface of the Earth where human beings tend to congregate – g will be a constant 9.81 ms-1, making the period T entirely dependent on the length of the pendulum l. The frequency is just the number of oscillations per second, and so when the pendulum swings at a period T we can find its frequency 1/T. This is the pendulum’s resonant frequency; the frequency of oscillation at which it will produce the largest oscillation for the smallest energy outlay. Since it loses only a tiny amount of energy with each swing (and that only because the point where the pendulum is attached to whatever it’s swinging from will not be frictionless, and if it’s swinging in an atmosphere you’ve also got the question of drag to consider) the pendulum will swing with that period for a long, long time – hence why pendulums “prefer” to swing at this period T determined by their length: it’s the most efficient way they can swing.
So resonance is motion where an object oscillates/vibrates in a way which ensures the maximum possible motion for the minimum possible energy outlay. Objects can have many different resonant frequencies (which are an integer multiple of the fundamental frequency) and resonance is crucial to the real world operation of many things – opera singers breaking wine glasses by vibrating their vocal chords at the glass’s resonant frequency; tuning forks which, when struck, will quickly settle down to resonating at a certain set pitch governed by their resonant frequency; and string instruments like pianos which rely on hammers hitting steel strings of different lengths held under tension which then vibrate at their resonant frequency, producing a single tone depending on the length of the particular string. It can also lead to some amusing mishaps when applied to large-scale engineering projects, like this one:
Now, there are differing views on whether Tacoma Narrows really was an example of resonance. My undergraduate physics textbook would have me believe that it was, while Font Of All Knowledge Wikipedia says that it was not. However, since there are recorded examples of bridges which have collapsed due to resonance from, e.g., army formations marching over them in lockstep, and that as a result of this resonance is one of the things engineers have to account for when building bridges these days, it’s as good an example as any to illustrate that minor, repetitive perturbations of an object can have a very powerful effect on that object if they happen to match one of its resonant frequencies thanks to the efficient transfer and storage of the object’s energy. This holds true even when those minor, repetitive perturbations are one planet gravitationally interacting with another planet as it orbits around the sun.
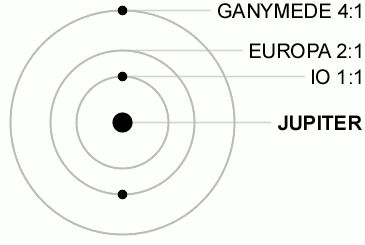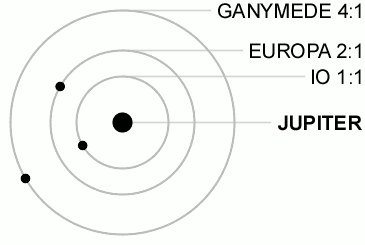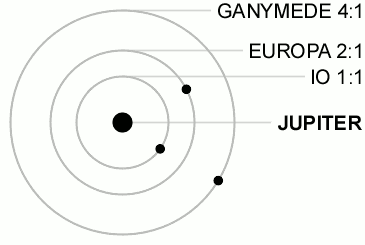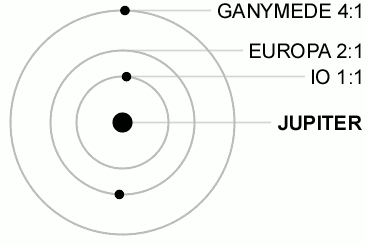
Here is an example of orbital resonance:
This is the 4:2:1 resonance between Ganymede, Europa and Io. (You can think of those numbers as integer numbers of some fundamental frequency that governs orbits, as with mechanical resonance.) As you can see, Europa orbits Jupiter twice for every orbit Ganymede makes, while Io orbits four times. This is called a mean motion orbital resonance because the ratios of the orbits of the moons are simple integers. Every time two of the moons are on the same side of the planet their mutual gravitational pull is greatly increased since they are closer together, with potentially catastrophic consequences.
Now, you may be thinking that it is something of a massive coincidence that Ganymede, Europa and Io just happen to have orbits that interlock so perfectly with one another, but it’s the same sort of massive coincidence that has led to you sitting here today reading the words that I have written. In other words, the Galilean moons did not just pop into existence in those positions and with those orbital resonances; they instead evolved over time until they reached their current stable, self-correcting orbits. We think of the Solar System as being immutable and unchanging, but that’s only over human timescales. Over million- and billion-year timescales the orbits of the planets and moons themselves change; this is either because they were not stable in the first place, or else because they are exchanging angular momentum with other, smaller bodies such as asteroids and comets (this will be important next week). For example, there’s a laser reflector on the Moon that the Apollo astronauts left behind that scientists use to very, very accurately measure how far the Moon is from the Earth. What they found was that the Moon is gradually slipping away from the Earth at the rate of 4 cm per year – this may not sound like much, but over millions of years it all adds up1. The orbits of the planets have similarly evolved and continue to evolve; as the Sun converts mass into radiative energy its gravitational hold on the planets will slacken and diminish, leading to them migrating further outwards in their orbits2. And the same sort of thing is true of Io, Ganymede and Europa, which started closer in to Jupiter and migrated outwards until they reached their current arrangement, at which point their positions became self-perpetuating thanks to the orbital resonance.
The 4:2:1 Galilean resonance is an example of a stable resonance that resists any change in the orbits of its component moons, but not all orbital resonances are like this. Many orbital resonances are destabilising resonances, where the repeated gravitational perturbation of having two bodies in close proximity during their orbits moves one of them out of its stable orbit and ejects it from the Solar System. The best way to think about this is by imagining the gravitational force between the two bodies as an impossibly long rope strung between them. Usually the rope is just taut and under tension, but whenever the two bodies pass close by to each other the big one gives an almighty tug on the rope, yanking the smaller one towards it. Over thousands of orbits these repeated tugs on the gravitational rope can drag the smaller body off of its orbital path and from that point on it’s bye-bye, Solar System.
You’ve probably seen the effects of resonance, even though you might not have known it at the time. The most famous example is the rings of Saturn, the structure of which is a product of both stabilising and destabilising resonances. The gaps in the rings are caused by a number of different things, and one of these things is a destabilising resonance with certain of Saturn’s moons that are orbiting in phase with that portion of the rings3. On the other hand some of the rings exist in orbital regions where they should have dissipated long ago, and this is thanks to stabilising resonances with – again — large moons such as Titan. Other not so obvious examples of resonance in the Solar System include the Kirkwood gaps in the asteroid belt, which are governed by mean motion resonances with Jupiter. And finally there’s Pluto, which exists in a 2:3 resonance with Neptune.
Now, normally Pluto could never exist where it does. It has an orbital path with a high eccentricity which crosses that of Neptune (again, this should have been a big hint that Pluto Isn’t A Planet). If it’s going that close to the orbital path of one of the gas giants it should have been booted out of the Solar System a long time ago. However, Pluto survives thanks to its 2:3 resonance; any time it gets close enough to Neptune that it starts to become a hazard, Neptune gives it a gravitational kick that speeds it up and shifts it to a wider orbit further away from Neptune. Conversely, any time Pluto looks like it might be getting far enough away from Neptune that it will escape this resonance, Neptune gives it another gravitational kick from the opposite direction that slows it down and corrects its orbit. So while the orbit of Pluto is constantly shifting over time thanks to interactions with Neptune, these interactions and orbital shifts cancel each other out leading to Pluto existing in this stable 2:3 resonance.
(This is illustrated with a pretty animated gif on this website if you’re having trouble visualising exactly what is going on. The orbital paths are plotted with respect to Neptune which is stationary from the gif’s point of view, so Neptune is the blue dot which never moves. The orbit of Pluto is in pink, with the Neptune-crossing part of its orbit represented as the loop, or “twist”. As you can see, any time this dangerous part of its orbit looks like it might get too close to Neptune – which would be fatal for Pluto – the gravitational interactions of the 2:3 resonance “corrects” Pluto’s orbit and shunts it back in the opposite direction.)
And that’s orbital resonance. Nearly all the examples of resonance we see in the Solar System today are stabilising resonances; destabilising resonances are generally indicated by the absence of stuff where stuff should be as per the Kirkwood gaps. With Jupiter and the other gas giants being as large as they are their orbital resonances have had a very significant effect on the way the Solar System has formed and evolved over time, and particularly so in the case of Pluto and the other TNOs that form the Kuiper Belt, the Scattered Disc and the Oort Cloud. Which was kind of the point in me explaining resonance in the first place: I cannot adequately describe those areas without explaining why they are structured the way they are, and I cannot do that without talking about resonance. HOORAY.
- The reason for this is tides, but not in the way you might think. Every time the Moon causes a high tide it creates a slight bulge in the ocean. This bulge is situated a little bit ahead of the Earth-Moon axis thanks to the rotation of the Earth, causing an uneven gravitational force that drags the Moon forward very, very slightly. The upshot of all this is that the Earth is losing rotational momentum to the Moon, which is converting it to orbital momentum and moving further away from the Earth. Wikipedia tells me that this interaction would in theory go on for another fifty billion years until the Earth and Moon become spin-locked in – what else – a resonance, but that the Moon will never get that far because the Sun is due to increase in size and luminosity and vaporise the Earth’s oceans 2.1 billion years from now. So that’s nice, I guess.
- This, incidentally, is why nobody has any goddamn idea what is going to happen to the Earth when the Sun gets big and strong and turns into a red giant.
- Other gaps are caused by moons orbiting inside the rings themselves, while the remainder are unexplained at this point in time.




[...] happened” is overwhelmingly likely to be the chaotic gravitational interactions, peturbations and resonances of the solar system’s early years. For example, there’s lots of very large, very conspicuous [...]
[…] (Thanks: http://scientificgamer.com/resonating-resonances/) […]