Ever wondered how we know how far away stars are? How we can estimate such colossally huge distances even though stars are, to us, just tiny pinpricks of light? Well too bad, you’re going to find out anyway.
If you want to measure the distance between us and, say, Betelgeuse, there are a number of hurdles that have to be overcome, chief of which is that starting out we have absolutely no idea how bright Betelgeuse is or how big it is. We know how bright it appears to be, but that on its own doesn’t tell us very much – after all, if you’re standing in the middle of a dark field at night at night a 20 watt lightbulb a hundred metres away will look exactly the same as an 80 watt lightbulb two hundred metres away. We can’t figure out how bright the star really is until we know how far it is away from us, and we won’t know how far away from us until we know how bright it is. It’s a bit of a catch-22, but fortunately there are a couple of ways to get around it and measure the distance using other methods. The first is parallax measurement.
Hold your finger up in front of your face. While keeping your finger still, move your head to one side. Then move your head to the other side. Your finger will appear to move against the background, even though it’s really staying in the same place. This is parallax, and we can measure the distance between the Earth and the nearest stars using exactly the same principle. A photograph is taken of a nearby star against the backdrop of the night sky when the Earth is on one side of the Sun. Six months later, when the Earth has orbited round to the other side of the Sun, a second photograph is taken of the star. The background stars — which are too far away to be affected by parallax — will remain in the same positions, and the near star will appear to move against this background. By calculating the parallax angle of the triangle formed by the Earth, the star and the Sun, it’s a simple matter of trigonometry to work out the distance to the star.
(This, incidentally, is where the term ‘parsec’ comes from. Parallax angles are measured in arcseconds, where an arcsecond is 1/360th of a degree. One parsec is the distance associated with a parallax angle of one arcsecond – so short for ‘a parallax of one second’ – and is equivalent to 3.26 light years, or about 30 trillion kilometres.)
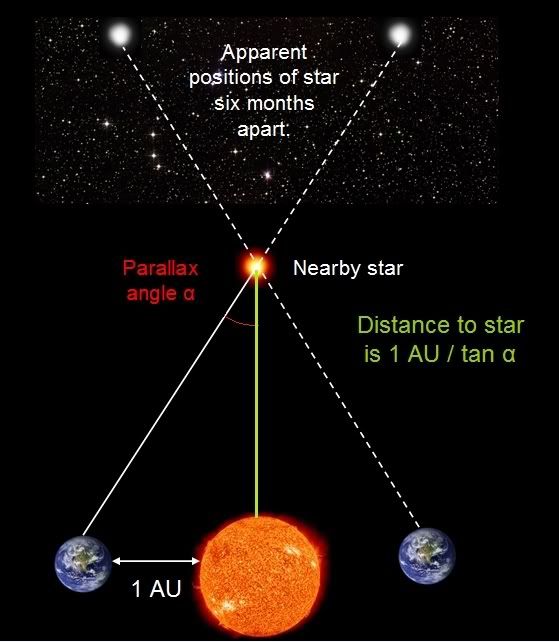
- And I bet you thought Pythagoras’ theorem was for suckas and chumps.
The parallax method only works for stars that are close enough to us to appear to have this motion relative to us as the Earth orbits the Sun. Despite this, it gives us a starting point: we know how bright some objects appear to be, we know how far away they are, and from this we can work out how bright they really are; this is their absolute brightness. We can then apply that knowledge to other observed objects that are further away that look like they might be in the same class – if they have the same absolute brightness, how far away would they be? This is the ‘standard candle’ method, and it varies in effectiveness depending on the object being used as the candle.
One of the most common types of standard candle – the ones used settle the question over the existence of other galaxies, for starters — are a type of star called Cepheid variables. Cepheids are unusual for stars because they don’t burn with a single more-or-less steady brightness, but instead they vary their brightness according to a fixed period; first they grow dimmer, then they get brighter, then dimmer, then brighter, and so on. This puzzled astronomers for many years, until Henrietta Leavitt Swann – who was a ‘computer’ engaged in the manual examination of thousands of photographic plates of stars, this sort of menial work being the only way women could get at serious astronomy at the start of the 20th century – realised there was a direct correlation between the brightness of a Cepheid variable and the time between the successive light pulses they gave off, otherwise known as the period of luminosity. After this it was just a matter of finding a Cepheid that was close enough to be measured by parallax (there are several including Polaris, the North Star) in order to get the absolute brightness. Once that was known, the distance to all other Cepheid variables could be determined from their period of luminosity.

- Science time! This is Henrietta Leavitt’s original study of the period-luminosity relation between 25 Cepheid variables in the Magellanic Clouds [Leavitt H., (1912). Periods of 25 variable stars in the Magellanic Clouds, Harvard College Observatory Circular, 173.]. The right-hand graph is the one we’re interested in, where the x (horizontal) axis is the absolute magnitude – or luminosity – of the Cepheids, and the y axis is the logarithm of their periods of luminosity. It’s a straight-line plot, proving a relationship between the two.
Another type of standard candle is the Type 1a supernova. This is an unusual type of supernova (although they are observed throughout the known universe) because it’s not caused by a star reaching the end of its life cycle and exploding, but instead by two stars merging with each other and… well, exploding. The trick to this one lies in the fact that white dwarfs are already the leftovers of supernovae explosions; after every supernova a small core remnant of the star will remain. What exactly happens to this core depends on its mass, but most core remnants go on to become white dwarfs: very small, dense star corpses that have a faint luminosity thanks to stored thermal radiation. Now, because white dwarfs have already gone nova they wouldn’t normally have the mass on hand to do it again – unless it was supplied by an outside source, like another star. So if you’ve got two stars orbiting one another in a binary star system, and one of them is a white dwarf which is slowly leeching mass off the other one, sooner or later it’s going to hit the trigger mass for a second supernova. This trigger mass is the same every time a type 1a supernova happens, with the result that every single type 1a supernova has the same absolute brightness which can be determined mathematically based on that trigger mass.
(For an incredibly bad analogy, imagine setting off a 50 kiloton nuclear warhead on the surface of the Moon. We’d know how bright the flash of the explosion should be based on the size of the warhead, so by comparing that with how bright the flash appears to us we can work out how far away the Moon is. I mean, if we really wanted to.)
There are many other types of standard candle but they all work roughly the same way. When trying to calculate the distance to some faraway star, astronomers will look for the closest standard candle and then make an estimate of the distance based on the distance to the candle (along with a very healthy error factor to cover the fact that they’re basically guessing). If we want to know how far away a galaxy is then all we have to do is find a standard candle inside it. However, this kind of distance measurement is subject to all kinds of error factors and assumptions, and so any time you see an astronomer on TV talking about something that’s 60,000 light years away, bear in mind that what they really mean is “somewhere between 40,000 and 80,000 light years away”.
Lastly there’s galactic redshift. This is based on Hubble’s law and the expansion of the universe; most galaxies are moving away from us at a fairly rapid pace, and this Doppler-shifts (stretches) the wavelength of the light those galaxies emit into the red part of the spectrum. The faster a galaxy is moving away from us, the more the light coming from the stars in that galaxy will be redshifted. This isn’t so great for measuring distance since redshift is a measurement of galactic velocity, not distance, but we do know that there’s a rough correlation between how far away things are and how fast they’re moving away from us. The most distant parts of the universe so far observed have very heavily redshifted light while the bits closer to us are less redshifted, so for stuff that’s too far away for standard candles to be of any use we can instead use the amount of redshift to give us an approximate distance to it.
So, uh, yeah. If you take anything away from this, it’s that astronomers are very clever people who are still basically making it up as they go along.



[...] problems are similar to the ones I mentioned in my post on stellar measurement; without doing something very clever there’s no real way of determining how big something is in [...]
[...] of Type 1a supernovae in distant galaxies (have I talked about standard candles before? I’m sure I must have) that those galaxies were actually moving away from us far faster than a simple model of a [...]
[...] and Triangulum (if you need Cepheid variables explained I go over them in one of my first posts here , and the Wikipedia article is here ) Hubble decided to see just how many other galaxies he could [...]