Josh, 7, from London, writes:
Dear Hentzau,
I went to the beach yesterday. The weather was nice. I had ice cream. When I was splashing around in the sea with my rubber ring wedged firmly around my waist to stop me sinking, I thought about the planets. Planets have rings, but they do not have to be prevented from sinking. Why do planet rings always go around the middle?
(And they do always go around the middle: see Uranus, which is tilted almost ninety degrees on its side but which has rings which still orbit around the equator.)
Well, little Josh, it’s because of three factors which shall be tackled in numerical order.
1) Planetary formation from a protoplanetary disc.
2) The Roche limit.
3) Planets are fat.
When a planet forms, it does so out of a big cloud of stuff. Much of this stuff is fairly hefty planetesimals (stuff one kilometre plus on a side) but there is lots of smaller stuff as well. The planetesimals along with the smaller stuff collapse towards the centre of the cloud towards the proto-planet core. As we’ve seen in the post on the Nice model, when you have a big cloud of stuff that’s shrinking it will start to rotate. Rotation produces centrifugal force, and centrifugal force will flatten the cloud out into a disc. Eventually you end up with the proto-planet at the middle surrounded by a big disc of stuff. What happens to the leftover stuff is determined by how close it is to the proto-planet.
- Stuff close to planet: falls onto planet.
- Stuff far away from planet: forms moons and stuff.
- Stuff in the middle: forms rings.
Now, clearly there are some niggling factors which mean it isn’t quite as simple as that, chief of which is that only the gas giants have rings (yeah some people think Rhea might also have rings but honestly screw those people). Earth, Mars and the other terrestrials don’t. This is because the size of the “stuff in the middle” category is dictated by something called the Roche limit.
The Roche limit is, broadly speaking, the orbital radius inside which the gravitational tidal force of the planet is greater than the gravitational force keeping whatever object has been unwise enough to venture inside it in one piece. In other words, if you go inside the Roche limit and gravity is the major force holding you together1 – so I don’t recommend this at all if you happen to be a planet or a moon — you get pulled apart. I like the Roche limit because it’s one of the few physical terms that I actually understand the derivation of, but I won’t go into that here. It’s expressed as an approximation by:
where R is the radius of the primary (i.e. the planet), ρM is the density of the primary, ρm is the density of the thing orbiting it, and d is the Roche limit.
So the Roche limit isn’t strictly a hard physical constant; it’s going to vary from body to body depending on the ratio of the densities of the primary and the orbiting body. However, because R is also in there, if you have a really, really big planet – like a gas giant, say – the Roche limit is going to be a factor no matter how dense your orbiting body is.
Using FABULOUS EXCEL TECHNOLOGY, I have created a graph which shows how the Roche limit varies with the density of the orbiting body for Saturn and Earth.
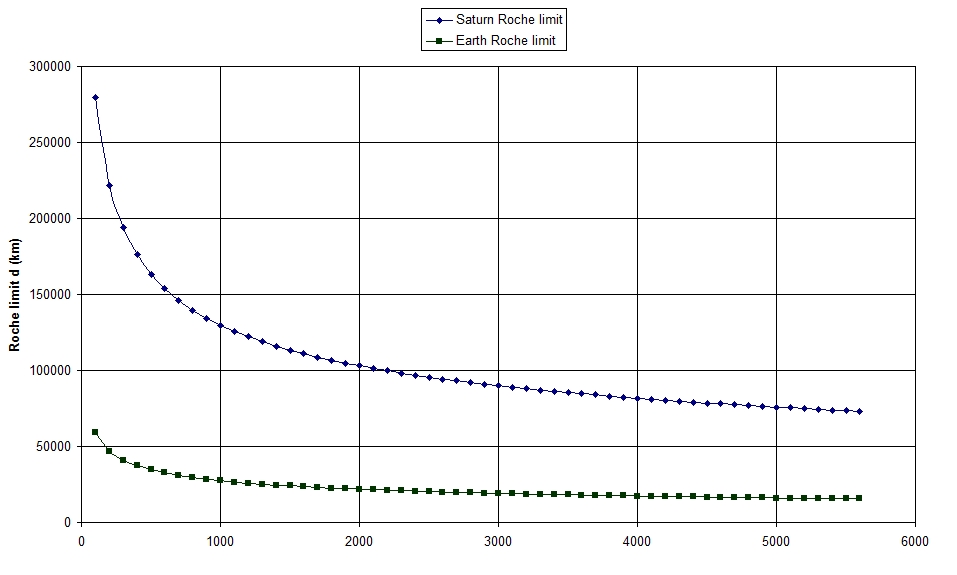
This makes it very easy to see that the Roche limit is big for less dense things and small for more dense things, and also that as you increase the density more and more it becomes practically static.
Now, to get the Roche limit for your proto-planet you have to put a number on the average density of protoplanetary material. I’m going to use the mass of a comet, which is about 500 kg m-3. This gives Roche limits of:
- Saturn: 160,000 km.
- Earth: 35,000 km.
35,000 km is sod all, in orbital terms. It’s just slightly less than the altitude at which we orbit geostationary satellites; any protoplanetary material orbiting inside 35,000 km is overwhelmingly likely to fall onto the proto-Earth anyway, so that explains why the Earth has no rings. The Roche limit of 160,000 km for Saturn on the other hand matches very nicely the observed outer edge of Saturn’s ring system.
This is where the bulk of planetary ring material comes from, then; they’re formed from the leftovers of planet formation that are far enough away to avoid falling onto the planet outright, but too close to the planet to form themselves into moons. Since this disc was rotating around the “equator” of the proto-planet anyway thanks to the cloud collapse, that explains why the rings are found there. However, this doesn’t answer an important question: what about ring material that was captured after planet formation? Say a comet ventures inside the Roche limit on a highly inclined trajectory. Why isn’t it pulled apart into a ring orbiting the planet at that inclination?
Well, this is where we come to the third thing on our list: planets are fat. Literally. Because they’re rotating objects centrifugal force distorts their shape away from the perfect sphere of hydrostatic equilibrium, making them slightly fatter around the equator than they are around the poles. For example, Earth has a radius 6,378 km around the equator but only 6,356 km around the poles; those 22 km may not seem like much but they make a big difference as far as orbiting bodies are concerned, because it means things that aren’t orbiting around the equator will nevertheless be pulled in that direction thanks to the extra mass that’s present there. Over thousands of years they’ll slowly migrate to the equator, at which point they’ll probably collide with some of the other junk that’s orbiting there which robs them of their orbital momentum and stops them where they are. Planets may be a little bit flabby around the waist, but if you like to look at ring systems a little extra weight is no bad thing.
In conclusion:
- The majority of planetary ring material forms around the equator of the planet in a disc.
- The inner edge of the rings is created by the planet, which drags material that gets too close towards it.
- The outer edge of the rings is created by orbiting moons, which sweep up material outside of the ring area.
- The rings themselves are defined by the Roche limit, which dictates the nominal area where ring material cannot form itself into moons because the planet is gravitationally dominant.
- All material added to the rings after planet formation migrates towards the equator thanks to the planet not being a perfect sphere and having more mass – and therefore gravity – distributed around the equator.
BULLET POINTS.
1. You might think of the Earth as a solid object but it isn’t really. It’s held together by gravity; no material could possibly provide the same amount of bonding force to keep all of its mass in one place. This goes for most large bodies out there; they’re so big that the only thing that can keep them in one piece is gravity, so if they come across something with a larger gravitational force then it’s bad news for them.





So what’s the significance of 2.44 in the Roche equation?
It means you should multiply R root cubed PM over Pm by 2.44.
(Seriously though, it’s just a number that pops out of the immensely complicated derivation for liquid bodies. There’s no real significance to it.)
Cool. Just thought it might have some significance.
[...] by Uranus’s gravity and then somehow reforming afterwards. If you remember my post about the Roche limit you should be able to figure out why this second assertion is bollocks: moons are pulled apart when [...]