Saying that I have a Ph.D elicits a fairly predictable reaction from most people. They will, in an attempt to appear interested, ask “What subject?” and then when informed that I did Astrophysics – one of the simpler branches of physics if you don’t tangle with cosmology or relativity but which appears to have a fearsome reputation in the eyes of the layman – their eyes glaze over and they either stop talking to me altogether, or else they desperately try to change the subject before I can get a chance to pounce on them, knock them to the ground and inject pure Science into their brains via their ear canal1. There’s a second type of person out there, however; the freakish sort who are genuinely interested in science, and this second type will, after some circumspect small talk, eventually get around to asking me what my thesis was about. And this is a question to which I have gradually evolved a tried-and-tested one-sentence reply:
“I am trying to find out how much energy you need to blow up Pluto.”
As with all one-sentence descriptions it doesn’t even come close to summing up the totality of my work, but it is accurate and it does its job of seizing their interest in an unbreakable choke-hold so that they ask the follow-up question:“Why?” Today, you’re all going to find out. You lucky, lucky people.
What does it mean to destroy something? Gormless techno-fetishist Michael Crichton inadvertently touched on why this is a bit of a tricky question in one of his godawful dinosaur novels, in which the shameless author self-insert of Ian Malcolm tells another character that his statement that nuclear weapons could destroy the world is really, really goddamn stupid. The reasons for this should be fairly obvious given the nuclear weapons post – while nuclear weapons pose a significant threat to humans, they could do very, very little to imperil the Earth. They’d scorch some parts of the surface, irradiate others, screw up the atmosphere for years – things that would have dire consequences for the future survival of the human race — but all this would amount to nothing more than a mild skin rash as far as the Earth is concerned. It’d just keep on truckin’ quite happily while we killed ourselves off.
Clearly you need a different magnitude of threat altogether in order to stand a decent chance of destroying the Earth. The sort of exotic cosmic catastrophe so enamoured of the Hollywood disaster movie notwithstanding (solar flares, quasars, supernovae, mini-black holes etc.), stuff smashing into other stuff is a thing that happens fairly often in our Solar System2. What happens if we hit the Earth with a really big space rock? Well, that’s actually happened. The Earth was hit by a Mars-sized object very early on in its lifetime. Mars-sized. The impact was so destructive we have a constant reminder that it happened in the form of the Moon. The impact was so destructive it blew off a majority of the Earth’s surface material. Yet even after this colossal impact event which would have fit most people’s criteria for “destruction” the Earth got better.
Key to this is that while the physical structure of the Earth was shattered by the impact, with bits and pieces flying in all directions, the heavy iron core was left mostly intact which meant the gravitational centre of mass of the Earth remained largely unchanged. Unless the impact fragments had been boosted up to escape velocity they were gradually and inexorably pulled back towards that centre of mass, with the result that the Earth slowly reformed much like Robert Patrick in Terminator 2. The Mars-sized impactor also left a remnant that accumulated bits and pieces of ejected surface material from the Earth; this went on to form the Moon, and it’s why the Moon is mostly made up of elements we’d expect to find in the Earth’s crust and mantle.
So even if you hit a planet-sized object really, really hard you’re not guaranteed to “destroy” it in any real sense of the term; you will disrupt its physical structure temporarily, but it may eventually reform into a single homogenous body again over millions of years. This destruction thing is a tricky business when applied to planets, and even when dealing with smaller stuff it’s difficult to draw a line. How much of an object do you have to destroy in order to say that the object itself is destroyed? A third? Two thirds? Total destruction? This is the first fundamental question that faces scientists who want to model impact events, and the answer they’ve come up with may seem arbitrary but it does have logic behind it.
First, impact scientists do not say impacts destroy something. We say they disrupt it, for the very good reason that disrupt is a term that can apply to any quantity of blown-off material, whereas saying something is destroyed runs into any number of problems up to and including the rather large one that matter cannot be created or destroyed, merely converted into energy. We define disruption by how much of the original body is left after we’ve whacked it with an impactor; in the case of my experiments I weighed my targets before they went into the gun, shot the crap out of them, and then weighed the biggest remaining chunk I could find afterwards. If that chunk was less than half the mass of the original body I’d rip open my shirt and beat my chest while let out an Arnie-in-Predator-esque roar of “DISRUPTION!”
The fifty-percent mark delineates disruption from cratering. If an impact removes less than fifty percent of an object’s mass it doesn’t count as disruption since the majority of the original object is still intact. Technically it’s a crater. It might be a really, really, really big crater – a crater that’s almost larger than the remaining mass of the body – but it’s a crater nonetheless. If the impact blows off more than fifty percent, though, it’s a catastrophic disruption outcome. This is as close to the word “destroyed” as you’ll ever get an impact scientist to go; personally I think the work in my thesis showed there’s a more granular range of impact outcomes than the simple binary choice of disruption and cratering described here, but my work was never published so eh.
So we’ve got a technical definition of “destroyed” now. In order to get there, we need to hit the object with enough kinetic energy to permanently disrupt more than 50% of its mass. Kinetic energy is worked out by the equation
where m is the mass of the impacting body and v is its velocity. Using kinetic energy allows us to make useful comparisons between an impact by a very small thing moving very quickly and an impact by a very big thing moving very slowly – i.e. it essentially makes the analysis independent of what the impactor actually is. We can further remove dependence on the size of the thing being hit by dividing the impacting kinetic energy value by the mass of the target; this gives the energy density of the impact, or Q, measured in joules per kilogram.
Q is, in theory, a very, very useful quantity. Say you have one target weighing 1 kilogram and another target weighing 1000 kilograms. By carrying out a series of impact experiments on 1 kilo targets in a lab environment you have determined that the energy density at which the 1 kilo target will lose more than 50% of its mass – the energy density at which it will suffer catastrophic disruption, or the critical energy density Q* — as 50 J kg-1. In theory, it should then be possible to predict how much energy it’ll take to disrupt the 1000 kilogram target without having to manhandle any one-tonne weights around your laboratory; you just multiply by a thousand and bam, that’s how much energy you need to pump into it to remove 50% of its mass. In theory, we can predict how planet-scale masses will behave under impact using the same measurement we took from the 1 kilo target.
In practice, though, it doesn’t really work like this. You have a number of factors that alter Q* depending on the size of the target. At first, as you make a target larger, it actually becomes easier to disrupt, pound for pound, than a comparable smaller target. This is because cracks propagate far more easily through large objects than they do small ones, and it is crack propagation that breaks off the huge chunks of material required for disruption. So Q* will initially decrease as target size increases. Then, when you’ve increased the mass of the target to the point where its gravity starts to become a significant factor (as explained in the Earth impact example above), this trend reverses itself. From this point onwards the bigger – and therefore heavier – the target, the harder it is to disrupt, since you’ve not only got to blow the thing apart but you’ve also got to do it with enough force that you give the majority of the fragments escape velocity.
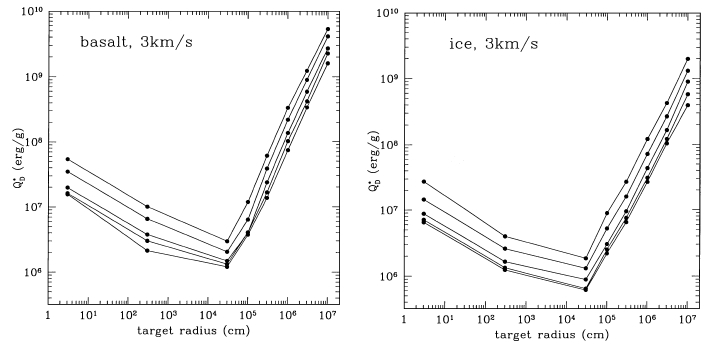
This is a graph from a paper published by Willi Benz and Eric Asphaug3 in 1999. Benz is a computer modeller while Asphaug does impact experiments in the laboratory; and they’ve combined their data in an attempt to put some numbers on how exactly Q* will change with target size. At first Q* decreases; the initial value of Q* and the rate at which it decreases will be heavily dependent on the material the target is made of – rock is harder to disrupt than ice, and so on – causing this to be referred to as the material regime. Then at target sizes of around 100 metres – 1 kilometre Q* starts to increase with target size; this is the gravitational regime. What’s really interesting about these graphs is that they’re for two wildly different materials – solid ice has a Q* of about 10 – 40 J kg-1, while basalt is roughly twenty times that – and yet the shift to the gravitational regime occurs at exactly the same place and in exactly the same way for each. This means that once you hit a target size of 100-1000 m, the material strength of the target has entirely ceased to matter when calculating the result of an impact. It is instead the body’s self-gravity which must be overcome in order to disrupt it
My, that all got a little bit technical. If you didn’t understand the fine detail don’t worry; I didn’t explain it that well and it’s not necessary to grasp all of it to understand what I was doing with Pluto. All you need to take away from it is this:
- We can do impact experiments in the laboratory to get a value for the amount of energy we need to hit a target with to blow it up.
- We can then take that energy value and, allowing for variations in Q* with target size as per the above graphs, scale it up to larger bodies to predict how much energy we’d need to hit them with to blow them up.
So that’s how I was trying to find out how much energy we’d need to blow up Pluto. But why Pluto? And why is it important? Unfortunately I’ve already rambled on a little more than I really intended to, and thinking about it I probably need to explain some additional background before I get on to that. So it will have to wait a week or two. Sorry!
- Presumably.
- Over a timescale of hundreds of millions of years, that is.
- Fun fact: I met Eric Asphaug at a conference in Spain and stole all his water.





Why Pluto? Because it is no longer a planet AND MUST BE DESTROYED.
That’s a dreadfully sizeist comment, Kenti. I expected better of you.
Hey, I didn’t make Pluto small. It did that all by itself!
This is amazing. Just leaving a quick comment so that I can come back and read your post in more detail…
Hmmm, I should have known there would be other scientists blogging on wordpress. I didn’t have any mice minions when I was doing my Ph.D, though. Now I feel like I missed out.
Yeah, but you were planning to blow up former planets! That’s got to count for something? Much more menacing than a mouse-army.
So how much energy does it take to blow up Pluto? THE SUSPENSE IS KILLING ME!
Less than it would take to blow up just about any other notable celestial object you can think of.
[...] 2) The critical energy density required to blow a body in the belt to smithereens without it eventually reforming under its own gravity. [...]