
Terraforming’s a bit of a thorny debate these days. Even leaving aside the question of whether or not we should be doing it in the first place — I once gave a talk where I referred to people who thought we should preserve the Martian surface as a sort of natural park as “crazy lunatics1”, only to have one of the other speakers come up to me afterwards and tell me he was one of them2 – there are many technological hurdles to be overcome, ranging all the way from raising/lowering the temperature of an entire planet to a liveable standard to generating a breathable atmosphere. While some of these hurdles are truly significant and will require decades – or even centuries – of technological advance before we can terraform a planet in any meaningful way, there’s also a lot of wilful obfuscation going on about just what is and isn’t possible in the first place. For example, some people will tell you that there’s no point in colonising and terraforming Mars because it’s too small to effectively retain an atmosphere. You should not trust these people, because they are lying – or at least, they are being very economical with the truth.
How do atmospheres work? As it turns out, the same way as everything else; that is, the gas molecules making up a planet’s atmosphere are bound to it by the planet’s gravity. However, there are some key differences. Inside the atmosphere all the different gas molecules are constantly moving around, colliding with each other, exchanging energy and then moving off in different directions. This means there are a couple of special rules that apply thanks to the difference in behaviour between a gas molecule and the unwieldy mass of squishy cells and organs that makes up the average human being. The general behaviour of a gas is described by the equation
![]() where P is the pressure of its gas, V is its volume, N is the number of molecules of gas enclosed in that volume, k is something called the Boltzmann constant and T is the temperature of the gas in Kelvin.
where P is the pressure of its gas, V is its volume, N is the number of molecules of gas enclosed in that volume, k is something called the Boltzmann constant and T is the temperature of the gas in Kelvin.
The Boltzmann constant is necessary because temperature is not a property that can be applied to an individual gas molecule. There is no such thing as a gas molecule with a temperature of 300K; instead, the molecule will be moving at such-and-such a speed which gives it a certain kinetic energy, which will be different from the speed and energy of an adjacent molecule in the same volume. This speed is constantly changing as the molecule collides with other molecules and loses or gains energy, making it impossible to get discrete speed/energy measurements for a single gas molecule. The only way we can deal with a gas in any meaningful sense is by measuring the average kinetic energy of all the molecules inside it; this is expressed as its temperature. So in order to convert temperature — a measure designed to describe the general behaviour of a whole bunch of gas molecules — to the energy of a single molecule of the gas, we need to chuck in the Boltzmann constant k. The general idea is that the quantity kT will be on the order of (that is, somewhere close to, but probably not the same as) the energy of a given gas molecule in the volume V.
Understanding the difference between temperature and the kinetic energy of a single molecule is important for understanding how atmospheres work. All the gas molecules in a planet’s atmosphere are whizzing around at completely different speeds and kinetic energies even though the atmosphere itself has a certain temperature T. Most of the molecule velocities will cluster around the molecule speed described by that temperature T, but there will be many, many outliers which travel slower or faster. The range of molecule speeds and how they change with temperature is described by something called the Maxwell-Boltzmann distribution.
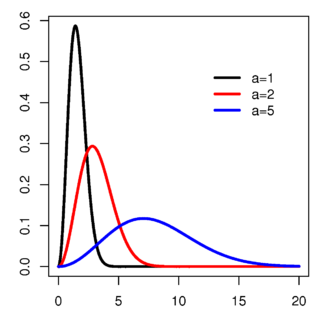 That graph may look a bit bewildering, but hopefully once I’ve explained what’s going on it won’t be all that complicated. The number on the vertical (or y) axis is the probability function, while the number on the horizontal x-axis is the speed of the molecule. What the graph is describing is what the probability is of a certain molecule in a gas travelling at a certain speed given a temperature a. If a single molecule has a 0.6 (or 60%) chance of travelling at a certain speed, then it follows that 60% of all the molecules in the gas will be travelling at that speed. The three different coloured plots on the graph show how this probability distribution changes at three different relative temperatures, a = 1, 2 and 5.
That graph may look a bit bewildering, but hopefully once I’ve explained what’s going on it won’t be all that complicated. The number on the vertical (or y) axis is the probability function, while the number on the horizontal x-axis is the speed of the molecule. What the graph is describing is what the probability is of a certain molecule in a gas travelling at a certain speed given a temperature a. If a single molecule has a 0.6 (or 60%) chance of travelling at a certain speed, then it follows that 60% of all the molecules in the gas will be travelling at that speed. The three different coloured plots on the graph show how this probability distribution changes at three different relative temperatures, a = 1, 2 and 5.
So from the graph we can see that for a low temperature of 1, all the gas molecules will be tightly clustered around a speed of 1-2, with none of them exceeding a speed of five3. Increasing the temperature to 2 changes the shape of the distribution; the average speed of a gas molecule is now 3-4 but the range of speeds at which the gas molecules as a whole travel is now much larger, as shown by the wider base and shallow peak of the distribution. Finally, for a high temperature of 5 the speeds of the gas molecules are much more evenly distributed, with a small peak at about 7 but with a long tail that stretches off all the way up to 15.
This long tail is the thing that interests us. Even if the temperature of an atmosphere is low, and the majority of the gas molecules in it are travelling at low speeds, some of the molecules will be travelling faster. A few of them will be travelling much faster – and if they’re travelling fast enough, they’ll reach what is called the planet’s escape velocity.
The escape velocity is a measure of how fast something has to be going in order to escape the planet’s gravity well permanently. You could strap yourself into a rocket and blast yourself into space, but if your rocket wasn’t powerful enough to propel you up to escape velocity before it ran out of fuel you’d eventually plummet back down to Earth if you didn’t manage to get into a stable orbit. The escape velocity changes from planet to planet as every planet has a different mass and therefore a different level of gravity, and furthermore since the gravitational force a planet exerts on an object diminishes the further away that object is from it, the escape velocity is greatest at the surface of a planet and diminishes as you progress upwards into space.
Now that we have all the background information down, we can finally start to look at why atmospheres are the way are. In reality atmospheres are not composed of a single homogenous gas but instead a whole variety of different elements. Even inside an atmosphere with a single uniform temperature the heavier gas molecules such as nitrogen and oxygen might have the same kinetic energy as a hydrogen molecule, but they’ll be travelling at lower speeds thanks to their greater mass. This causes the various gaseous elements inside an atmosphere to differentiate themselves according to weight; the heavier, slower stuff can’t get very far off the ground and is found close to the surface, while the lighter molecules can and slowly migrate to the higher portions of the atmosphere over time. If a molecule is light enough and the air around it is thin enough (so that it doesn’t get its direction of travel changed by a collision with another molecule) then the velocity of that molecule can easily exceed the planet’s escape velocity and escape into space – and this is true even if the temperature isn’t high enough for the average velocity of a gas molecule to exceed the escape velocity because the long tail of the Maxwell distribution ensures that some of the molecules will be moving fast enough, causing the planet to slowly (or not so slowly) bleed portions of its atmosphere away into space.
How likely a given molecule of gas is to remain part of the atmosphere can be calculated mathematically. My notes here don’t go into the specifics of how the Maxwell distribution and the interactions between molecules dictate this, but if a molecular constituent’s thermal velocity is near one-third the escape velocity, then about half of that molecule type will have escaped from the atmosphere within weeks. If the thermal velocity is one-fifth of the escape velocity, then the planet will lose half of that molecule type after a billion years. And if the thermal velocity is one-tenth of the escape velocity, then the planet will retain that molecular constituent indefinitely.
Therefore we run two parallel equations.
where G is the gravitational constant and k is the Boltzmann constant.
Everything in these equations that isn’t a number or a constant is a property that affects the likelihood of a planet losing a certain type of gas – the mass of the planet, the radius of the planet (since gravity diminishes the further away you go from the centre of mass), the temperature of the atmosphere and the mass of the gas molecule. If, at the end of the day, vthermal is more than 0.1 vescape, the planet will eventually lose that gas type. How much more vthermal is is what dictates how quickly this happens.
From this the compositions of the atmospheres of the planets become much clearer. Earth has very little hydrogen or helium in its atmosphere because it’s not massive enough to hold on to them. Jupiter has no such problems (not to mention forming in an area where light materials were much more abundant) and so it’s still got most of its primordial hydrogen – this is why Jupiter and the other outer planets are referred to as gas giants. Mars is a relatively light planet and so much of its atmosphere has seeped away over time, but it still retains a fair amount of the heavier stuff such as carbon dioxide. Poor old Mercury gets hit with a double whammy: not only is it situated very close to the Sun — raising its surface temperature and thus its escape rate — but it’s also constantly being blasted by the solar wind which also serves to strip away atmosphere, as a result of which it doesn’t really have one any more.
So how is this all relevant to the terraforming argument? Well, if we run the equations above for an oxygen molecule in the Martian atmosphere we get a mean thermal velocity of 630 metres per second. Mars has an escape velocity of 5 kilometres per second. While Mars is losing oxygen molecules to thermal escape over time it’s doing it very slowly. This means that the fact that Mars has a crappy atmosphere in terms of potential human habitation has very little to do with how small it is, and is in fact heavily related to two other factors:
- Attrition by the solar wind; something we don’t have to worry about so much here on Earth thanks to the magnetosphere.
- Mars getting absolutely creamed by asteroid/comet impacts (along with every other terrestrial planet) during the Late Heavy Bombardment. Like, so much so that there’s still chunks of Mars dating from around about then floating around the Solar System which occasionally fall to Earth. This is because the impacts were so violent they threw up ejecta and debris from the surface so high and so fast that they reached escape velocity and were never seen again. From the point of view of Mars, anyway. If the Late Heavy Bombardment did that sort of thing to solid rock, imagine what it did to the atmosphere.
The first point is something that any prospective terraformers would still have to worry about, and given the lack of any magnetosphere on Mars the solar wind is likely to contribute far more to atmosphere loss than thermal escape. Barring some sort of cataclysmic event we don’t have to worry about the second ever happening again, at least over human timescales. As a result, while any Martian atmosphere we generate would dissipate relatively quickly, that “relatively” is relatively to the lifetime of the planets and the Solar System. In timescales relevant to humans even the most pessimistic estimates have a usable Martian atmosphere sticking around for 200,000 – 300,000 years, and it’s more likely that it’d last for a million plus. Are we really going to say terraforming the Martian surface isn’t worth it because the atmosphere will “only” last for 300,000 years?
1. It was a talk for kids aged 12-16 so I couldn’t say what I really thought of them.
2. The moral of this story is either that you should never use even mild language like “crazy lunatics” in case there are some crazy lunatics in your audience, or else that no matter what you do you should be prepared to go through life inadvertently offending an awful lot of people.
3. This graph uses dimensionless measures because the shape of it will be the same no matter what system of measurement you use to measure the temperature and speed of the gas.




So…. when do we begin the terraforming then?
Probably a couple of centuries from now. Sooner, if population pressure and dwindling resources provides sufficient incentive.