(Click on that for the full picture. DO IT. DO IT NOW.)
This question plopped into my inbox like a month ago now.
Name: Justin M.
Question: How can physicists determine the shape of the universe, and what implications might the different speculated shapes of the universe have?
And I’ve been avoiding it ever since, because if you mean what I think you mean it’s an insanely hard subject to try to explain to somebody who hasn’t done, say, three years of an undergraduate physics degree course.
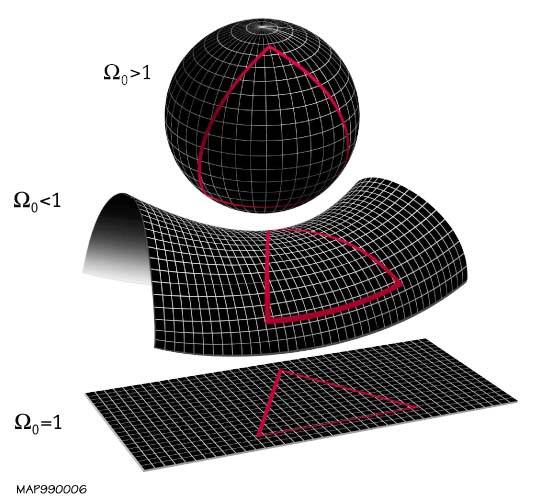
Now, if I’m lucky you just want to know about the old open/closed/flat conundrum. That I can do. We will start with this picture, swiped from the usual source:
These are the three possible candidates for the general shape of the fabric of the universe: football, pringle or bedsheet. Other scientists call these closed, open and flat respectively. I call them boring. Exactly what is going on here is quite easy to visualise in my head but as soon as I try to put it into words bad things happen, but I’ll have a go just for you.
When Einstein first worked out the fundamental concept of general relativity he also came up with a bunch of equations – called the Einstein field equations – which describe how gravity works in a universe where the fabric of spacetime is warped and curved by the presence of matter and energy. Einstein did his general relativity work before Edwin Hubble showed that the universe was expanding through galactic redshift measurements and the Big Bang had yet to be accepted as common scientific orthodoxy, so he assumed we lived in a static universe (i.e. one that is not expanding or contracting) just like the rest of the scientific establishment. The problem with this was that if you start off with a universe that is in perfect static equilibrium, general relativity says that that universe will inevitably start to contract due to the mutual gravitational attraction of everything in it. As it stood general relativity simply didn’t allow for the concept of a static universe, so in order to make his field equations work he fudged them slightly by adding in something called the cosmological constant which provided the universe with a fundamental internal pressure that resisted the contraction due to gravity.
This may have made Einstein’s equations balance and allowed him to model his static universe, but it was bad science and he knew it. After the expansion of the universe was proven he famously referred to the cosmological constant as the biggest blunder of his life; if he’d had faith in the robustness of his theory he could have predicted an expanding universe long before it was confirmed experimentally. Anyway, in an expanding universe the cosmological constant was nothing more than a curio, a simple artefact of the maths. It didn’t have any relevance to anything that was actually physically happening and a lot of people simply ignored it.
That was up until 1998, when it was discovered through redshift measurements of Type 1a supernovae in distant galaxies (have I talked about standard candles before? I’m sure I must have) that those galaxies were actually moving away from us far faster than a simple model of a continually expanding universe would seem to imply, and that the most distant parts of the universe were accelerating in their rate of expansion. This accelerating universe model has since been confirmed by, amongst other things, observations of fluctuations in the cosmic background radiation by the Wilkinson Microwave Anisotropy Probe (WMAP) in the 2000s. An imperfect way of describing this CMB anisotropy is as an “echo” of the Big Bang – the CMB is leftover radiation from the formation of the universe, and the fluctuations in its structure essentially make up a record of the distribution of matter in the universe just after the Big Bang. Circumstances have changed a bit since then, of course, and by comparing the positions and velocities of galaxies now to the CMB rest frame we can get the closest thing possible to an “absolute” measure of galactic velocity. These velocity measurements appear to show that the universe is indeed accelerating in its expansion.
This is interesting for a number of reasons, but the one we’re mainly concerned about is that in the basic expanding universe model without a cosmological constant there are two factors governing the rate of expansion: the inertia of expansion provided by the Big Bang, and the gravitational attraction of all the matter inside the universe counteracting that. Depending on how much stuff there is in the universe and how closely it’s packed together (density), there are three possible outcomes for this basic model.
1) There is enough gravity to overcome the expansion inertia. The expansion of the universe will gradually stop and reverse itself, and everything will collapse into a Big Crunch. This is a closed universe.
2) There isn’t enough gravity to overcome the expansion inertia. The universe continues to expand, everything becomes more and more spread out and diffuse, and things inevitably end in widespread entropy and heat death. This is an open universe.
3) There is just enough gravity to counterbalance the expansion inertia. The expansion rate of the universe will continually slow, gradually approaching zero without ever quite getting there. This is a flat universe.
Note that in none of these three models is there any room for the expansion of the universe accelerating somehow. Clearly there’s something up with it that needs fixing. Serendipitously, though, if you drop Einstein’s previously-defunct cosmological constant back into the cosmological model, it turns out that you can model the accelerating expansion of the universe. The acceleration is driven by the outwards pressure that the cosmological constant represents. And by fiddling with the parameters of the cosmological constant, we can describe something approximating the universe we see today.
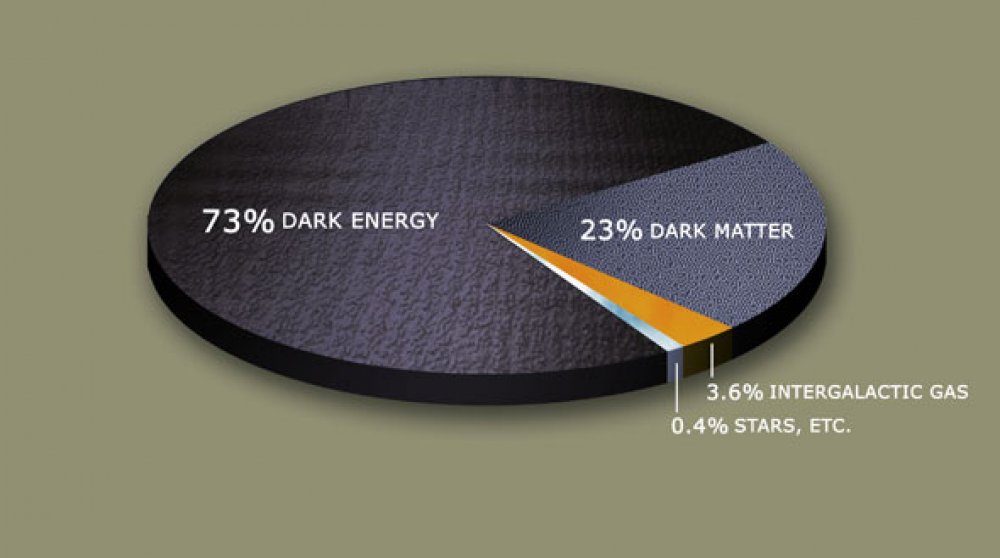
What is the cosmological constant, though? Where is this outwards pressure it describes coming from in physical terms? The short answer is: dark energy. Exactly what that is nobody really knows; all we know for sure is that there must be some sort of intrinsic energy permeating all of space (sometimes called vacuum energy if you’re particularly into sci-fi) that counterbalances gravity and causes this acceleration in expansion. I can’t give you a great explanation of dark energy since it really is at the cutting edge of theoretical cosmology, so if you want to find out about it I recommend you read this bit on Wikipedia and then go from there. All I can tell you is that while we cannot perceive the dark energy itself, we can certainly perceive its effects: accelerating expansion, which requires some tinkering with the basic cosmological model I described above in order to accommodate it.
When you dump the cosmological constant back into the model you end up with what is today called the Lambda-CDM model of the universe, which is the currently-accepted model of How Things Are. It’s called Lambda-CDM because lambda is the mathematical symbol representing the cosmological constant, while CDM stands for Cold Dark Matter. Both of these things are needed to explain inadequacies in the previously-accepted model of the universe, the FLRW metric. Lambda-CDM is FLRW on steroids; it doesn’t replace FLRW so much as it supplements it and makes it work with the current observational evidence. The expansion of the universe is governed by lambda, the cosmological constant, as well as baryonic and dark matter (for gravity). The idea is that you add the shit out of all these subcomponents and you get a final number, omega, which tells you what is going to happen to the universe at the end of time, and also incidentally what it happens to be shaped like.
Hey, I knew we’d get back here eventually. That number to the bottom left of each possible universe shape is omega, or Ω. Omega is the observed density of all the stuff in the universe divided by the theoretical critical density required for a perfectly flat universe. If Ω adds up to be bigger than one, then you get the closed beachball universe. If it’s less than one then you get an open pringle universe. If it happens to be exactly one, then you get a flat bathtowel universe. The outcomes are roughly the same as described above, except with the addition of the cosmological constant the pressure due to dark energy eventually overcomes gravitational attraction in the flat model, causing the universe to first slow down in its expansion and then speed back up again once gravity has been smacked down sufficiently, and things end up just like an open universe: in entropy and heat death. The role this shape — or geometry — plays beyond being linked to the expansion and fate of the universe is somewhat explained here if you read the bits about triangles and angles and parallel lines.
As it happens the WMAP probe also measured the overall geometry of the universe (if you want a “how?” then you can start with this), and it came back with the answer that Ω was equal to 1 with less than 0.5% error. In other words the part of the universe that we can see appears to be almost perfectly flat with very little local curvature. However, since we don’t know how much of the universe we can see it could be that this only holds true for our little corner of it. Saying that the universe is flat now would be like ancient civilisations saying that the world was flat; it certainly looked flat, but that was just because they could only see part of it and it was actually way bigger than they thought.
So yes. After like a hundred years of modern astronomy and cosmology, we can finally say that the bit of the universe we live in is probably mostly flat. QED.
(Christ I just realised I managed to get all the way through this post without mentioning Friedmann at all. That’s a massive fault on my part.)
PS – I’m out of questions now so feel free to send more in. I mean, you don’t have to if you don’t want to. But it would be nice.