
Black holes. Sexiest of all the holes.
Wait no that came out completely wrong. What I was trying to say there was that black holes have this rather exotic reputation amongst the population at large, mainly because various sci-fi films have given them all sorts of weird and wonderful attributes – they’re portals to other universes, they’re mechanisms for time travel, they’re power sources for starships etc. etc. They seem to capture the imagination rather more handily than any other celestial object before or since, and so I thought I’d spend a little bit of time talking about them.
What is a black hole?
It’s an odd little region of space created by a whole bunch of mass scrunched up very small into a single point called a singularity. Gravitational force is inversely proportional to the square of the distance separating you from an object’s centre of mass as per
where G is the gravitational constant, M is the mass of the larger body, m is the mass of the smaller body (usually negligible where massive stellar bodies are concerned) and r is the distance between the two.
Note: it’s been pointed out to me that it’s possibly easier, instead of just chucking the m away because it’s very small, to shift it over to the F side of the equation. Since F = ma it then follows that F/m = a, meaning GM/r^2 = a, or acceleration. If you’re having trouble visualising what I mean when I say “The gravitational force is such-and-such N/kg,” try imagining it in terms of acceleration instead.
Thanks to the r2 in that equation the force that a massive body like, say, the Sun exerts on you is usually comparatively small. Even if you went all the way to the surface of the Sun it would still be comparatively small, because the Sun is very big and you’ve still got about 695,000 km between you and the Sun’s centre of mass. Gravitationally speaking the Sun is a bit of a weakling; in terms of its heat and energy throughput you’d be burned to a crisp before you ever got that far, though, so it’s probably wisest not to stow thrones in grass houses.
Now consider the Sun if it were scrunched up into one of these singularities. A singularity outputs no radiation and has no surface to stop infalling objects, so it’s possible for us to get much, much closer to the singularity than we would a regular stellar object. Even though the singularity has a similar amount of mass to the Sun and hence exerts a similar level of gravitational influence at 695,000 km distance, as we approach the singularity itself the gravitational force it exerts on us is going to increase exponentially as r decreases. Eventually, if the singularity is massive enough, we will get close enough that the gravitational force it exerts will become so great that the required escape velocity will be more than the speed of light in a vacuum. And since light can no longer escape the singularity’s pull, everything inside this radius will appear completely featureless and black to an outside observer. We now have our black hole.
It is important to note that the black hole is not the singularity. The singularity is merely the bit in the centre where all the mass is, while the black hole is everything encompassed inside this region of space that we cannot see. The border of the black hole is defined by the event horizon — so called because we can’t see any event that happens past it, just like we wouldn’t be able to see somebody waving to us over the Earth’s horizon – but the event horizon is not the “surface” of the black hole. It’s possible for an object to fall past the event horizon and still have a perfectly good time in the few moments remaining to it until it hits the singularity. The event horizon merely marks the point of no return; the radius inside which you will at some point become part of the singularity no matter what you do.
How is the radius of the event horizon defined?
In its simplest form, by something called the Schwarzchild radius, which applies for a perfectly spherical non-rotating singularity. We can derive this from the equations for gravitational potential energy and kinetic energy; the radius of the event horizon will be the point where the gravitational potential energy of the black hole exactly equals the kinetic energy of the light, or
where m is the “mass” of the light (light has no mass, but that doesn’t matter because that term’s going to be removed from the equation in a minute anyway), v is the velocity of the light (commonly expressed in physics as c, which is equivalent to 300,000 km s-1), M is the mass of the singularity, R is the distance at which the gravitational force is acting (in this case equivalent to the Schwarzchild radius Rc since that’s the point at which kinetic energy equals gravitational energy) and h is the distance of the light from the gravitational souce (again, equivalent to Rc). Substituting these values into the above equation and cancelling out redundant ones gives us
which rearranges to
Since c and G are constants, the radius of the event horizon is therefore directly proportional to the mass of the singularity, and Wikipedia has saved me the trouble of crunching numbers by telling me that this proportionality is equivalent to a radius of 2.95 km per solar mass. In other words, if you really did go to the trouble of scrunching the Sun up into a singularity, its event horizon – and therefore the radius of the black hole it would create – would be just 2.95 km from the centre.
What’s interesting about the Schwarzchild radius is that increasing the mass of the singularity will increase the Schwarzchild radius on a linear 1:1 basis (i.e. one solar mass gives an Rc of 2.95 km, two solar masses gives an Rc of 5.9 km etc.), but it won’t do the same for the gravitational force that mass exerts at the Schwarzchild radius, since that is determined by
The best way to illustrate this is as follows: if we plug in the values Mo (representing one solar mass) for M and 2.95 km for Rc, we get
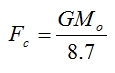 If we then double Mo (and hence double Rc) we get
If we then double Mo (and hence double Rc) we get
Despite doubling the mass of the singularity the force our hypothetical singularity exerts at the Schwarzchild radius has been halved, since by doing so we’ve doubled the Schwarzchild radius as well and gravitational force diminishes in proportion to the inverse square of the distance from the source.
The upshot of all this is that you may or may not be ripped apart before getting to the event horizon depending on the size of the singularity. A small black hole like our solar mass one would kill you well before you ever hit the event horizon since the Schwarzchild radius is so small, while you could get quite some way inside the event horizon of the supermassive black hole at the centre of the Milky Way before succumbing to tidal forces. Which brings me to…
What happens to you if you fall into a black hole?
Why, you die, of course! However, you do it somewhat earlier than you might think. You won’t survive long enough to splatter onto the surface of the singularity like a bug on a windshield, and you might not even make it past the event horizon; instead, sooner or later, you succumb to something called spaghettification.
Spaghettification is a rather comically unpleasant process where the immense tidal forces of the black hole stretch approaching objects out into very long, thin strands of matter kind of like spaghetti. Going back to the gravitational force equation mentioned above, the difference in the force exerted on either end of an object approaching the black hole will be
where G is the gravitational constant, M is the mass of the black hole, R is the distance separating the black hole and the bottom of the object, and L is the length of the object. Basically you’re subtracting the force the black hole exerts on the top of the object from the force the black hole exerts on the bottom of the object to find the tidal – or “stretching” – force. These kinds of tidal forces have a negligible effect on our day to day lives because the Earth doesn’t have much mass and we’re far enough away from its centre that we never even notice them; for a typical 170cm tall person walking around on the surface, the Earth will exert a tidal force of 5 x 10-6 N/kg (in other words, your feet will be pulled towards the centre of the Earth 5 x 10-6 m s-2 faster than your head), which is tiny, and anyway the surface of the Earth stops things from going any further.
However, if you up the mass of the thing you’re walking around on things start to get a bit more noticeable. If we replace the Earth with a singularity with the mass of the Sun, and recalculate the tidal force for the same distance away from the centre of mass (6400km), we find that our hypothetical singularity will pull the average person’s feet away from their head with a tidal force of 1.7 N/kg – this may not sound like much, but it’s roughly equivalent to half the maximum acceleration of a Saturn V rocket. I’m not sure if this would be fatal because the breaking force of a person isn’t listed anywhere on the internet for some reason, but it would definitely be uncomfortable and it’d only get worse as you fell further towards the singularity.
Anyway, even a very very small Sun-sized singularity will exert extreme tidal forces on objects close to it. These tidal forces are so strong (they increase to infinity as an object approaches the singularity, so there’s no way of resisting it) that any object which falls into a black hole will eventually end up being stretched out into the spaghetti-like strands described above.
What about relativistic effects?
I’m not going to talk about relativistic effects inside the event horizon, because nobody really knows how those work and the best hypotheses we have are a little bit wack. As ever with relativity, though, you have to consider two frames of reference; that of an outside observer, and that of the unlucky person actually going through the even horizon. For the latter, everything seems normal, although since they will be looking at the black hole from the inside it will be impossible for them to determine when they’ve crossed the event horizon (black holes don’t look black from the inside since there’s a whole bunch of light trapped in there with you). For the former, the person travelling towards the event horizon will appear to get slower and slower as the gravitational potential of the singularity increases and time dilates (they will also be redshifted) and they’ll never actually appear to hit the event horizon. This phenomena has been used to varying levels of effect in a number of bad sci-fi shows, almost all of which got it completely wrong.
If no light can escape the event horizon, how do we detect them?
A number of different methods, mostly revolving around their interactions with surrounding matter. Sometimes we can detect them through their simple gravitational effect on nearby bodies, but more often we see some sort of exotic stellar phenomena that can only be explained by the presence of a black hole. X-ray binaries, for example, are thought to consist of one normal star that is being gobbled up by a companion black hole; as the black hole chews up the star the infalling mass releases gravitational potential energy and spits it out in the form of very strong X-ray emissions, making this particular types of black hole very luminous in the X-ray spectrum.
The accretion discs surrounding “active” black holes that are in the process of consuming matter create X-rays by way of a similar mechanism: friction within the disc causes angular momentum to be transferred outward, which causes the gas in the disc which has lost that momentum to fall inward, which releases gravitational potential energy, which heats the gas up, which eventually gets so hot it starts emitting electromagnetic radiation in the X-ray part of the spectrum. Accretion discs are also sometimes accompanied by relativistic jets of matter that are blasted out from the poles of the black hole (thought to be caused by the shape of the hole’s magnetic field); these jets can sometimes be hundreds of light years in length, so they’re relatively easy to stop.
I should stress that nobody has ever directly observed a black hole. If it’s not actively consuming matter it’s practically impossible to spot one; you could theoretically do it by looking for gravitational lensing effects – caused by the black hole bending light as it passes by the outer edge of the event horizon – but this has never been done in practice. So for all we know the above phenomena could be alien firework displays or magic space rocks or something. The evidence pointing towards the concrete existence of black holes is largely theoretical, albeit very convincing.
How are black holes formed?
Or the more popular version of this question I used to be asked a lot, which is “Will the Sun ever become a black hole?” It was encouraging since it was usually 12-13 year old kids doing the asking and it showed they had grasped some of the basics of how black holes form, but the actual mechanism is a little bit complicated. Basically you need some way of squishing a lot of mass up really really small, and the commonly accepted way of doing this is via a supernova. And since supernovae are an entire post all by themselves, this thrilling cliffhanger seems like as good a place as any to stop. BUY THE SEQUEL! COMING SOON (on Thursday).

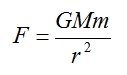


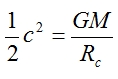
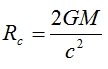
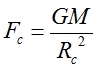




I can never get my head around the fact that light is a thing which can be affected by gravity. Light seems to be so intangible that a physical force being able to affect it is completely alien to me.
It may be ethereal and intangible and very, very nippy, but it still has to travel along the fabric of space-time to get to where it’s going. If that’s distorted by a large gravity well it gets deflected just like everything else.
See, I read and understand that but my brain still goes “bleurghh”.
Do we have any idea what would happen if lots and lots of matter splattered onto the singularity. Lots and lots and lots and lots until it all became much bigger? Does it then become less black-holey?
Or am I missing something obvious?
If lots of matter goes into a black hole the mass increases and so does the “size” of it (ie the event horizon expands). However, the singularity remains singularityish. The simple way (though not necessarily strictly accurate) way to think of it is that the gravity of the singularity is strong enough that the new matter is compressed into the same space as the singularity. Of course, a singularity sort of doesn’t have a volume by its nature but I think you probably get a bit quantum when you get down to that level.
I’ll be going into more detail on this on Thursday but: the gravity of a black hole is so great that it’s not just scrunching up atoms into a very small space, but it’s actually breaking down the structure of the atoms themselves. All those electrons, protons and neutrons are crushed together and the Pauli exclusion principle ceases to apply. Once you’ve overcome the natural repulsive forces keeping the component parts of atoms — and atoms themselves — separate, there’s nothing stopping you from compressing any amount of matter down into a single point. As Chris says quantum mechanics would probably have something to say about this, but this is one of the areas where general relativity does not mesh well with quantum mechanics.
If I remember correctly Pauli’s exclusion principle is quantum in itself in that it is about not allowing two particles to have the same quantum state. And I suspect its this gap betwen relativity and quantum mechanics which is why there is so much speculation with respect to exciting effects of black holes. After all, nobody can prove me wrong(TM).
Rather than saying “m is the mass of the smaller body (usually negligible where massive stellar bodies are concerned)” I think it would be much better if you instead just commented that acceleration is force over mass so removing m from the right side gives you the acceleration (which is something much more meaningful for most people). That way your later equation of the difference in force would be difference in acceleration.
Also I was sad that you didn’t actually do anything with that second equation except quote it there. I can do the maths myself but you did seem to just quote the equation without actually then talking about it much.
Both valid criticisms; the first is a result of me unconsciously thinking that way anyway and forgetting that few other people do as well, and the second is because I wrote this post in two sessions and the bit on the Schwarzchild radius was something I forgot to come back to. I’ll have a tinker with it in a bit.
I have to admit I will probably go and tinker with the maths myself. In particular rearranging that tidal equation to try to make it more obvious what the relative effects of L and X are. And because I remember in school working out stuff to do with the escape velocity and stuff and I can’t offhand remember how to do it. And because its fun. It’ll give me something to do on the bus on the way home.