Having explained the basic concept of gravitational barycentres, I can now get to the meat of what I wanted to talk about: Lagrange (or Lagrangian) points.
If we can find the gravitational barycentre between two objects, we should in theory be able to predict how they move based on their current position, velocity and their mutual gravitational position. Most of them time it’s not that simple, however. For instance, if we really want to plot the orbit of the Moon around the Earth, and do it accurately, we need to take other significant gravitational influences like the Sun into account. Predicting the orbital motion of the Earth-Moon-Sun system as they undergo mutual gravitational interactions is an example of what’s called the three-body problem, and it’s one that physicists and mathematicians have been trying to solve since the 17th century. While solutions for special cases of the three-body problem have been found a general solution for all cases is still very much beyond us, and increasing the number of gravitational influences still further (up to n bodies, which is known as the n-body problem) makes things even worse. We can simulate the interactions of n-body systems using very powerful supercomputers but this is only an approximation, and it’s possible that the n-body form of the problem has no solution since the approximation involves an infinite series of expansions that has to be truncated at some point in order to get a finite answer; in other words, solving the n-body problem is kind of like trying to find the exact value of pi.
Lagrange points rise as part of the three-body problem, but happily it’s one of the special cases we have an exact solution for known as the restricted three-body problem. In the restricted version of the problem the third body has negligible mass in comparison to the other two – it’s a probe or an asteroid rather than a moon or planet – and so exerts practically no gravitational force on the other two bodies in the system. The problem therefore becomes one of figuring out how the two bodies that do have mass affect the movement of the third massless body, and since the solution to the two-body problem is known this is something we can do.
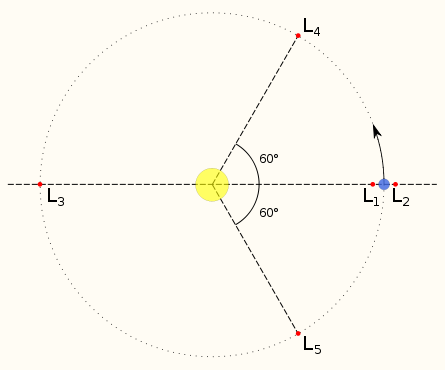
One quirk of the solution to the restricted three-body problem is that it indicates there are certain places where you can put the massless object that will cause it to – given the appropriate velocity – orbit the common barycentre of the system at the same rate as the two objects with mass. This is a fancy way of saying that it will be stationary with respect to the two massive objects and will be located at the same position relative to them at any point in their orbital system. These stationary points are called the Lagrange points, and there are five of them for every two-body system. For examples I’ll use the Earth and the Sun as my two-body system since they’re easy to understand, but Lagrange points also exist for the Earth and the Moon, the Sun and Jupiter and so on.
L1: Situated directly in between the Earth and the Sun, very close to the Earth. This is the point where the gravitational forces of the Earth and the Sun “balance”. Stuff orbiting closer to the Sun will do so at a faster velocity and over a shorter period, while stuff orbiting further away will orbit at a slower velocity and over a longer period. Ordinarily anything placed at the L1 point would orbit the Sun more quickly than the Earth and would thus be asynchronous with it; however, L1 is in just the right spot for the Earth’s gravity to provide a slowing force on any hypothetical body placed there that causes it to orbit the Sun with the same orbital period as the Earth.
L2: Like L1, but backwards. An object at L2 would ordinarily orbit the Sun more slowly than the Earth due to being further away; this time, though, the gravitational pull of the Earth works in the opposite direction, giving the L2 body a boost in speed and (again) causing it to orbit the Sun with the same orbital period as the Earth.
L3: Directly on the opposite side of the Sun to the Earth, L3 does not lie on the Earth’s orbital path as the diagram suggests; instead it’s just inside it as a result of the Earth-Sun barycentre being shifted slightly towards the Earth. L3 is the point where the combined gravitational pull of the Sun and the Earth act along the same line and provide a single unidirectional force that is equivalent to the gravitational force the Sun exerts on the Earth, causing an object placed there to orbit the barycentre just like the Earth does.
L4 + L5: The trickiest Lagrange points to explain, L4 and L5 lie at the apexes of a pair of equilateral triangles which have the Earth and the Sun as two of their corners. Objects at L4 and L5 are the same distance away from the Earth as they are from the Sun, forming an equilateral triangle! I was going to explain exactly how this happens but it involves trigonometry which I’m sure everyone is doing their damndest to forget, so I’ll just steal the following picture from Wikipedia.
Right, so, here the examples are the Earth and the Moon; the gravitational force of each combines into a single resultant force which is deflected to a point slightly away from the centre of mass of the Earth which just happens to be the barycentre of the Earth-Moon system, causing objects placed at L4 and L5 to – again – orbit the barycentre along with the Earth and the Moon.
So that’s what Lagrange points are and why they are. Why are they important? Well, the examples I used of our massless third body being an asteroid or a probe weren’t just for fun since that’s exactly the sort of thing that tends to be present at a Lagrange point.
L1: In the Earth-Sun system a probe placed at L1 will never be out of sight of the Sun (i.e. no eclipses by the Earth), making it very useful for solar observatories. In the Earth-Moon system you can stick a space station up there and use it as a halfway house for lunar exploration. I mean, if you really wanted to.
L2: Opposite of L1 (again); a probe at L2 will have almost all of the solar radiation from the Sun blocked by the Earth, so this is where we want to put space telescopes for the best result since solar radiation is the space equivalent of light pollution from cities. The successor to the Hubble, the James Webb space telescope, is going to be put at the Earth-Sun L2 when they eventually get around to finishing the damn thing.
L3: Kind of boring! It does kind of amuse me though because this is where some people thought you might be able to hide a secret planet; since it’s on the other side of the Sun it’d always be out of sight of the Earth. These people did not take into account the massive gravitational perturbations such a secret planet would cause, nor the fact that L3 is inherently unstable and no object can persist there over solar system timescales.
L4 + L5: You know how Jupiter gives asteroids, comets etc. that have the temerity to venture inwards towards the Sun a massive gravitational slap that sends them careening out of the Solar System towards parts unknown? The L4 and L5 points in the Jupiter-Sun system is where the lucky survivors of this process tend to congregrate; each of them is populated by a cluster of asteroids (well, I say cluster, there’s like a million of them) which are collectively referred to as the Trojans, and which make the asteroid distribution in the Solar System look like this.
The reason the Trojans are spread out over a fairly large area is that the regions around the L4 + L5 points where you can get a stable orbit are actually pretty large. This image maps gravitational potential as contour lines; while the L1, L2 and L3 points are all tight gravitational troughs, the L4 and L5 points are broad gravitational peaks that an asteroid can, with a bit of luck, perch on top of over long timescales (millions of years) without too much difficulty.




Interesting!
I’m glad you think so, because I have been writing this thing on and off for the last week and couldn’t even think of a decent way to finish it.. Would be a shame to see the effort wasted.
Sometimes I forget that our solar system has more than just planets in it. That last picture makes the place look quite crowded.
It both is and isn’t. In terms of number of objects, the solar system is very full. In terms of number of objects over space occupied, it’s incredibly sparse.
Yeah – really good article on an interesting topic. It is fairly hard to picture these interactions without a good explanation.
Could you park a theoretical spaceship at L3 to keep it hidden?
Very interesting read. One question: In the last diagram there is a label called “Hildas” where, it appears, a bunch of material is also hanging out. Is this the result of the L3 point for Sol-Jupiter?